стандартный потенциал, физико-химическая величина, условно характеризующая равновесную разность потенциалов между электродом и раствором в том случае, когда вещества, участвующие в электродной реакции, находятся в стандартном состоянии, т. е. их активности (активные концентрации) равны 1. Поскольку фактическая разность потенциалов электрода и раствора недоступна измерению, пользуются величинами, характеризующими потенциалы различных электродов относительно некоторого электрода сравнения. Обычно электродом сравнения служит нормальный Водородный электрод (Н. В. Э.), потенциал которого принимается равным нулю при любой температуре. Потенциал электрода, заряжающегося отрицательно относительно Н. В. Э., имеет знак минус, заряжающегося положительно - знак плюс. Совокупность Н. п. реакций разряда-ионизации металлов и водорода, расположенных в порядке их возрастания, называется рядом напряжений. Элементы с менее положительными Н. п. вытесняют элементы с более положительными Н. п. из раствора, содержащего их катионы. Н. п. вычисляют из результатов измерений эдс гальванических элементов, а также из стандартных значений изменения гиббсовой энергии (См. Гиббсова энергия) (свободной энергии) ΔG° при реакции. Величины Н. п. могут быть использованы для вычислений ΔG° и констант равновесия химических реакций. Такие вычисления необходимы для оценки возможности протекания химических реакций и для термодинамических расчётов (см. Термодинамика химическая).

Лит.: Киреев В. А., Краткий курс физической химии, М., 1963, гл. XIII, § 175; Справочник химика, т. 3, М. - Л., 1965; Перельман В. И., Краткий справочник химика, 6 изд., М., 1963; Гороновский И. Т., Назаренко Ю. П., Некряч Е. Ф., Краткий справочник по химии, 3 изд., К., 1965.

то же что Нормальный потенциал.

одно из современных уточнений понятия Алгоритма, получившее распространение в исследованиях по конструктивной математике (См. Конструктивная математика). Предложено в 1950 А. А. Марковым, впервые систематически и строго построившим на основе этого уточнения общую алгоритмов теорию (См. Алгоритмов теория). Н. а. эквивалентны частично-рекурсивным функциям (см. Рекурсивные функции), а следовательно, и Тьюринга машинам.

Концепция Н. а. специально приспособлена для реализации алгоритмов, действующих над словами в тех или иных алфавитах. При этом под алфавитом в математике понимается любой конечный набор четко отличимых друг от друга графических символов (букв), а под словом в данном алфавите - произвольная конечная цепочка букв этого алфавита. Цепочка, вовсе не содержащая букв, также считается словом в данном алфавите (пустое слово). Например, цепочки "ииаам", "книга", "гамма" являются словами в русском алфавите, а также в шестибуквенном алфавите {к, н, и, г, а, м}. Элементарным актом преобразования слов в алгоритмических процессах, задаваемых Н. а., является т. н. операция "подстановки вместо первого вхождения". Пусть Р, Q, R - слова в некотором алфавите. Результатом подстановки Q вместо первого вхождения Р в R называется слово ∑ (R, Р, Q), получаемое следующим образом. Если Р входит в R, т.е. R представимо в виде S₁PS₂, то среди таких представлений отыскивается представление с наиболее коротким словом S₁ и полагается ∑ (R, Р, Q) = S₁QS₂. Если же Р не входит в R, то ∑ (R, Р, Q) = R. Так, ∑ (гамма, а, е) = гемма.

Для задания Н. а. необходимо фиксировать некоторый алфавит А, не содержащий букв "→" и " · ", и упорядоченный список слов вида Р → Q (простая формула подстановки) или Р → · Q (заключит. формула подстановки), где Р и Q - слова в А. Формулы подстановок принято записывать друг под другом в порядке следования, объединяя их слева фигурной скобкой. Получающаяся фигура называется схемой Н. а. Исходными данными и результатами работы Н. а. являются слова в А (сам Н. а. называется Н. а. в алфавите А). Процесс применения к слову R Н. а. со схемой вида

где δ_i (1 ≤ i ≤ n) означает "→" или "→", разворачивается следующим образом. Отыскивается наименьшее i, при котором P_i входит в R. Если все P_i не входят в R, то работа заканчивается и её результатом считается R. Если требуемое i найдено, то переходят к слову ∑ (R, P_i, Q_i). При этом в случае, если использованная формула подстановки P_iδ_iQ_i была заключительной (δ_i = → ), работа заканчивается и результатом считается ∑ (R, P_i, Q_i). Если же формула P_iδ_iQ_i - простая, то описанная процедура повторяется с заменой R на ∑ (R, R_i, Q_i).

Пример. Натуральные числа можно рассматривать как слова в алфавите {О, 1} вида 0, 01, 01l,... Н. а. в этом алфавите со схемами {0 → · 01 и {1→ переводят каждое натуральное число п соответственно в n + 1 и в 0.

Множество всех Н. а. замкнуто относительно известных способов комбинирования алгоритмов. Например, по любым двум Н. а. и 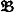можно построить Н. а. , являющийся композицией и , т. е. реализующий следующий интуитивный алгоритм: "сначала выполнить алгоритм , затем к результату применять ".

Соотношение между интуитивными алгоритмами и Н. а. описывается выдвинутым А. А. Марковым принципом нормализации: всякий алгоритм, перерабатывающий слова в данном алфавите А в слова в этом же алфавите, может быть реализован посредством Н. а. в некотором расширении А. [Легко указать очень простые алгоритмы в А, не реализуемые Н. а. в A; с другой стороны, всегда можно ограничиться двухбуквенным (и даже однобуквенным) расширением A.] Принцип нормализации эквивалентен тезису Чёрча и, аналогично последнему, не может быть доказан из-за неточности интуитивной концепции алгоритма.

Лит.: Марков А. А., Теория алгорифмов, М. - Л., 1954 (Тр. Математического института АН СССР, т. 42); Мендельсон Э., Введение в математическую логику, пер. с англ., М., 1971.

Б. А. Кушнер.